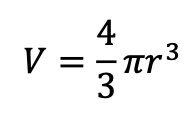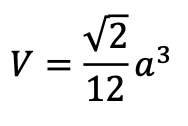【高校受験】正四面体の体積を求める公式

CONTENTS

こんにちは。添田です。

先日好物の数の子をネットで1kg購入しました。

大量の数の子に囲まれる日々はこの上なく幸せなのでみなさんもぜひ買ってみてください。

 

今回は正四面体の体積を求める公式を紹介します。

空間図形の問題で非常に役に立つのでぜひ覚えてください。

 

正四面体の体積を求める公式

体積を求める公式といえば，以下の球の体積の公式が有名です。

・半径rの球の体積V

受験生はもちろん知っていますね。

これと同様に正四面体の体積は以下の公式により求めることができます。

・一辺aの正四面体の体積V

覚えておくととても便利です。以下，導出過程を説明します。

正四面体の体積の公式の導出

正四面体は4つの面がすべて同じ正三角形の三角錐です。

図のような一辺の長さがaの正四面体ABCDを考えます。

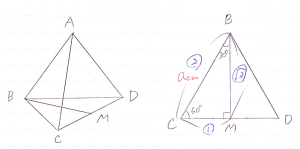
まず，底面の△BCDの面積を求めます。

△BCDの高さはBMになります。BMの長さは図のような比になる直角三角形なので，

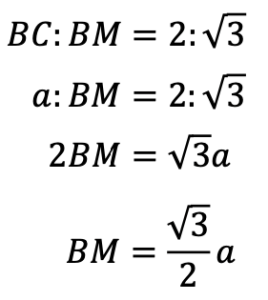
になります。よって，

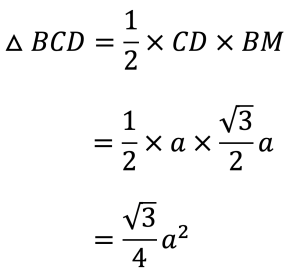
次に，正四面体ABCDの高さAGを求めます。

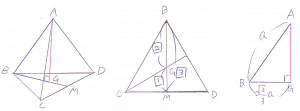
ここで，点Gは△BCDの重心でありBMを2:1に内分する点です。よって,

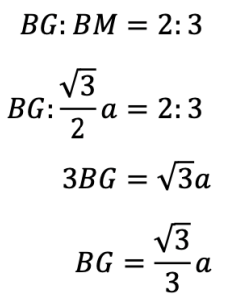
と求められます。よって，△ABGにおいて三平方の定理より

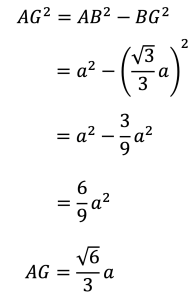
となります。よって，一辺をaとする正四面体の体積Vについて

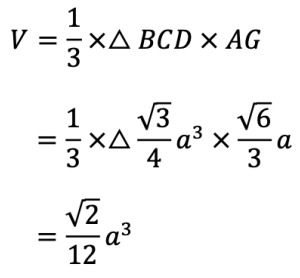
が導かれます。

 

このように正四面体の体積の導出は意外と複雑になりますので公式として暗記してしまってください。

また，正四面体と底面を共有する立体の体積は，この公式で求めた正四面体の体積に底面積の比および高さの比を乗ずることで求められます。

球の体積の導出

ちなみに，球の体積の公式は以下のように導出します。

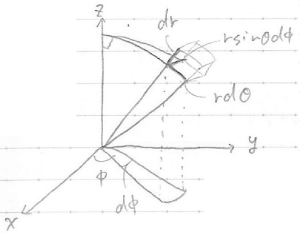
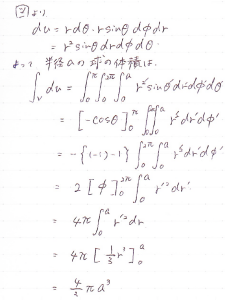
うっかり公式を忘れてしまった人は球座標系で上の図のように微小体積を求め，球の範囲を過不足ないように三重積分して計算してください！