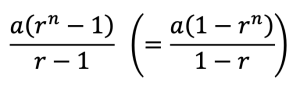【数列】1,11,111,1111,…の一般項と和の求め方

こんにちは。添田です。

今回は数列の問題を解説します。

福島大学の2次試験でも出題されたことのある有名問題です。

・問題

  次の数列{a_n}の一般項と第n項までの和を求めよ。

1, 11, 111, 1111, …

面白い数列ですね。数列の一般項と和を求める問題です。

まず等差数列でないのは明らかなので等比数列かどうか確認します。

・等比数列になっている？

初項と第2項に注目して初項1，公比11の等比数列を計算すると

1, 11, 121, 1331, 14641, …

となります。

これはこれでパスカルの三角形によって計算できる二項係数のような数列になっていて面白いですが，題意とは異なります。等比数列の公式で計算することはできません。

＜解法＞

この問題ではまず数列{a_n}の各項を桁ごとに分けた足し算の形に変形します。

1, 1+10, 1+10+10², 1+10+10²+10³, 1+10+10²+10³+10⁴, …

ここで数列の各項に注目するとそれぞれが初項1，公比10の等比数列の和になっていることがわかります。

{a_n}は「数列の和の数列」です。よって，一般項を求める段階で等比数列の和の公式を用います。

 初項a，公比r(r≠1)の等比数列の和

この公式に，a=1，r=10を代入すると，一般項a_nは

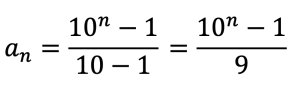
と求められます。

 

・数列の和の数列の和

この数列の和，すなわち「数列の和の数列の和」は𝛴を用いて計算します。

求める和をSとすると，

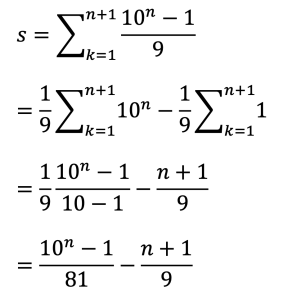
となります。

＜別解＞

問題の数列は階差数列でも一般項を求めることができます。階差数列{b_n}をとると

10, 100, 1000, 10000, …

となり初項10，公比10の等差数列になるので

b_n=10ⁿ

と求められます。

よって{b_n}の初項は1なので，n≧2のとき

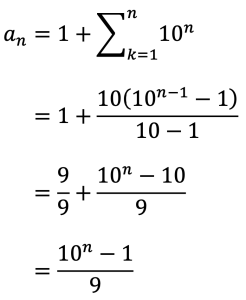
となり前述と同様の一般項が求められます。また，n=1のときも成立します。

・まとめ

1が1つずつ増えていく面白い数列を紹介しました。

等差数列や等比数列にならない問題も諦めず，頭をひねってみると面白い解法が見えてくるかもしれません。